The Rhombicuboctahedron is a captivating Archimedean solid, a harmonious dance of squares and triangles. It features 26 faces in total: 18 square faces and 8 triangle faces. These faces meet at 24 uniform vertices, with each vertex surrounded by one triangle and three squares (a configuration often denoted as 3.4.4.4). It possesses 48 edges, and its entire structure reveals a perfectly symmetrical polyhedron of balanced beauty.
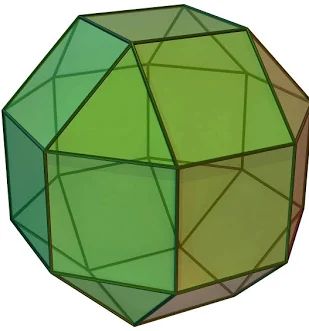
This remarkable shape can be derived from either a cube or an [octahedron) through a process of expansion. More specifically, it can be obtained by expanding a cuboctahedron (another Archimedean solid) by pulling its faces apart and inserting new square faces in the gaps. Its dual polyhedron is the Deltoidal Icositetrahedron, a shape with 24 kite-shaped faces. The Rhombicuboctahedron exhibits octahedral symmetry, reflecting its close relationship to the cube and octahedron, and is a uniform polyhedron.
The name "Rhombicuboctahedron" hints at its geometric origins. The "rhombi" part refers to the square faces, and "cuboctahedron" refers to the cuboctahedron, from which it can be expanded. It is a convex polyhedron, meaning all its interior angles are less than 180 degrees. This shape appears in various contexts, from the facets of crystals to components in mechanical design and architecture, showcasing its practical and aesthetic appeal.